In previous section, we talked about what is Bézier Curves, what are the various applications area, and how to write functions for generating control points for linear and bilinear curves.
Lets now see how we can write code for Cubic Bézier Curves
Cubic Bézier Curves are 3rd degree curves to explain this type curve, you will need to specify four points.
- Two anchor points (say P1 and P2) these are the starting and ending points of the cubic curve.
- Two control points (say C1 and C2) these are control points which tells curve how fast or slow curve should leave these points.
Above image shows the basic Cubic Bézier Curve example. Artists who use Adobe Illustrator or Macromedia Freehand will recognise a cubic curve.
and who don't understand what I am talking about the will understand eventually as will will proceed forward.
So next thing is how can we find point on Cubic Bézier Curve. To achieve this we can use de Casteljau algorithm. Which is named after engineer Paul de Casteljau (born 1930 in Besancon, France) he developed this algorithm for evaluating calculations on certain family of curves, which later popularized by engineer Pierre Bézier.
This algorithm is widely used, with some modifications, as it is robust an numerically stable method for evaluating polynomials. So lets find the points.
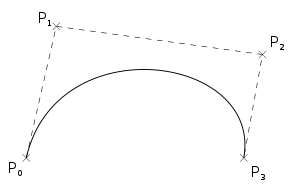
Finding points on a Bézier curve using de Casteljau algorithm
Each point of a cubic Bezier point corresponds to a value between
0 and 1 for a parameter that will be noted with t in the followings. The de Casteljau algorithm consists of the following simple steps:- Consider a Bézier curve with control points
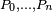 . Connecting the consecutive points we create the control polygon of the curve.
. Connecting the consecutive points we create the control polygon of the curve. - Subdivide now each line segment of this polygon with the ratio
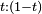 and connect the points you get. This way you arrive at the new polygon having one fewer segment.
and connect the points you get. This way you arrive at the new polygon having one fewer segment. - Repeat the process until you arrive at the single point - this is the point of the curve corresponding to the parameter
 .
.
The following picture shows this process for a cubic Bézier curve:
Note that the intermediate points that were constructed are in fact the control points for two new Bézier curves, both exactly coincident with the old one. This algorithm not only evaluates the curve at  , but splits the curve into two pieces at
, but splits the curve into two pieces at  , and provides the equations of the two sub-curves in Bézier form.
, and provides the equations of the two sub-curves in Bézier form.
 , but splits the curve into two pieces at
, but splits the curve into two pieces at  , and provides the equations of the two sub-curves in Bézier form.
, and provides the equations of the two sub-curves in Bézier form.
The interpretation given above is valid for a non-rational Bézier curve. To evaluate a rational Bézier curve in 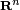 , we may project the point into
, we may project the point into 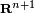 ; for example, a curve in three dimensions may have its control points
; for example, a curve in three dimensions may have its control points 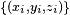 and weights
and weights 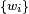 projected to the weighted control points
projected to the weighted control points 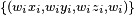 . The algorithm then proceeds as usual, interpolating in
. The algorithm then proceeds as usual, interpolating in 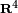 . The resulting four-dimensional points may be projected back into three-space with a perspective divide.
. The resulting four-dimensional points may be projected back into three-space with a perspective divide.
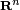 , we may project the point into
, we may project the point into 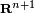 ; for example, a curve in three dimensions may have its control points
; for example, a curve in three dimensions may have its control points 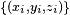 and weights
and weights 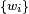 projected to the weighted control points
projected to the weighted control points 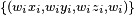 . The algorithm then proceeds as usual, interpolating in
. The algorithm then proceeds as usual, interpolating in 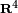 . The resulting four-dimensional points may be projected back into three-space with a perspective divide.
. The resulting four-dimensional points may be projected back into three-space with a perspective divide.
In general, operations on a rational curve (or surface) are equivalent to operations on a non-rational curve in a projective space. This representation as the "weighted control points" and weights is often convenient when evaluating rational curves.
Here's the code to generate the points from the definition of the curve, we will use recursion for this, most of the code is self explanatory:
Here's the code to generate the points from the definition of the curve, we will use recursion for this, most of the code is self explanatory:
// Calculate and Draw point from Casteljau Bezier algorithm
private void DrawCasteljau(List<point> points)
{
Point tempPoint;
for (double dt, dt <= 1; t += 0.001)
{
tempPoint = GetCasteljauPoint(points.Count-1, 0 , t);
image.SetPixel(tempPoint.X, tempPoint.Y, color);
}
}
// Calculate and Draw point from Casteljau Bezier algorithm
private void DrawCasteljau(List<point> points)
{
Point tempPoint;
for (double dt, dt <= 1; t += 0.001)
{
tempPoint = GetCasteljauPoint(points.Count-1, 0 , t);
image.SetPixel(tempPoint.X, tempPoint.Y, color);
}
}
In if( r == 0) return points[i]; code line we are returning point value at index i. So, if r is 0 then it just return the point as is without calculation and if i == 5 then points[5] will return the point in the array that is at index.
Conclusion
Here we learned about Cubic Bézier Curves and how to find the points using de Casteljau algorithm for such curves. In next blog will explore more and I will provide example unity project of Bézier Curves written in C# language. I hope you got some more insight on Bézier Curves.
References
- http://en.wikipedia.org/wiki/B%C3%A9zier_curve
- http://jeremykun.com/2013/05/11/bezier-curves-and-picasso/



![Animation of a linear Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/8/89/Bezier_1_big.gif/240px-Bezier_1_big.gif)
![Animation of a quadratic Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2d/Bezier_2_big.gif/240px-Bezier_2_big.gif)
![Animation of a cubic Bézier curve, t in [0,1]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/ff/Bezier_3_big.gif/240px-Bezier_3_big.gif)
